ไฟฟ้ากระแสสลับ

การกำเนิดไฟฟ้ากระแสสลับ

ค่าของแรงดันไฟฟ้ากระแสสลับจะเกิดขึ้นมากหรือน้อยนั้น ขึ้นอยู่กับตำแหน่งของขดลวดตัวนำขณะหมุนตัดกับเส้นแรงแม่เหล็กในสนามแม่เหล็กนั้น ถ้าทิศทางการเคลื่อนที่ของขดลวดตัวนำตั้งฉากกับเส้นแรงแม่เหล็ก แรงดันไฟฟ้าที่เกิดขึ้นจะมีค่าสูงสุดและจะมีค่าน้อยลง เมื่อทิศทางการเคลื่อนที่ของขดลวดตัวนำตัดกับเส้นแรงแม่เหล็กในมุมน้อยกว่า 90๐ และจะมีค่าเป็นศูนย์เมื่อขดลวดตัวนำวางขนานกับเส้นแรงแม่เหล็ก



จะเห็นว่าใน 1 วัฎจักรของการหมุนขดลวดตัวนำ คือ หมุนไป 360๐ ทางกลน้ำจะเกิดรูปคลื่นไซน์ 1 ลูกคลื่น หรือ 1 วัฎจักร ถ้าขดลวดตัวนำนี้หมุนด้วยความเร็วคงที่และสภาพของเส้นแรงแม่เหล็กมีความหนาแน่นเท่ากันตลอด รอบพื้นที่ของการตัดแรงดันไฟฟ้าสลับรูปคลื่นไซน์ที่จะมีค่าคงที่และถ้ามีการหมุนของขดลวดต่อเนื่องตลอดไป จะทำให้เกิดจำนวนรอบของแรงดันไฟฟ้าเหนี่ยวนำต่อเนื่องกันไป นั่นคือการเกิดแรงดันไฟฟ้ากระแสสลับ



ค่าแรงดันไฟฟ้ากระแสสลับชั่วขณะ

ค่าแรงดันไฟฟ้ากระแสสลับชั่วขณะ คือ ค่าของแรงไฟฟ้ากระแสสลับรูปคลื่นไซน์ ที่เราวัดได้ในแต่ละมุมของการหมุนของขดลวดตัวนำในเครื่องกำเนิดไฟฟ้า โดยมุมของการเคลื่อนที่นี้วันเป็นองศา ซึ่งค่าของแรงดันชั่วขณะสามารถหาได้จากสมการ



เมื่อแบ่งการหมุนของขดลวดตัวนำใน 1 วัฎจักร (360๐) เมื่อคำนวณค่าแรงดันชั่วขณะที่เกิดขึ้น ณ มุมต่างๆ ตั้งแต่ตำแหน่ง 0 ( 0องศา) ตำแหน่ง 1 (30 องศา) และตำแหน่ง 2, 3, 4 จนถึงตำแหน่งที่ 12 โดยเพิ่มค่ามุมทีละ 30๐ เราจะได้รูปคลื่นไซน์ของแรงดันไฟฟ้าสลับที่เกิดขึ้นมีขนดดังรูป






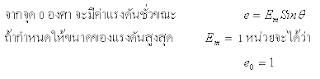
ความถี่และคาบเวลาของไฟฟ้ากระแสสลับ

ความถี่ของกระแสสลับ (Frequency ตัวย่อ f) หมายถึง จำนวนวัฏจักรของการเกิดรูปคลื่นไซน์ต่อเวลา 1 วินาที



ถ้าเกิดรูปคลื่นไซน์ 2 วัฏจักรต่อเวลา 1 วินาที ก็แสดงว่าไฟฟ้ากระแสสลับที่เกิดขึ้นมีความถี่ 2 วัฏจักรต่อเวลา 1 วินาที หรือเรียกแทนในหน่วยเฮิรตซ์ (Hz) หรือความถี่ไฟฟ้ากระแสสลับ 50 เฮิรตซ์ ก็คือการเกิดรูปคลื่นไซน์จำนวน 50 วัฏจักรต่อเวลา 1 วินาที และจากรูป 4.2 รูปคลื่นไซน์นี้มีความถี่เท่ากับ 1 เฮิรตซ์ เป็นต้น


ความถี่และคาบเวลาของไฟฟ้ากระแสสลับ

ค่าต่างๆ ที่สำคัญของรูปคลื่นไซน์ นอกจากความถี่และคาบเวลานั้นมีอีก 4 ค่า คือ ค่าสูงสุด(Maximum) ค่ายอดถึงยอด(Peak-to-Peak) ค่าเฉลี่ย(Average) และค่าใช้งาน(Effective)






ค่ายอดถึงยอด วัตถุจากจุดยอดของรูปคลื่นไซน์ด้านบวกจนถึงจุดยอดของรูปคลื่นไซน์ด้านลบ นั่นคือ ค่ายอดถึงยอดเท่ากับ 2 เท่าของค่าสูงสุด
ค่าเฉลี่ย ค่าเฉลี่ยของรูปคลื่นไซน์นั้นเราพิจารณาเฉพาะด้านใดด้านหนึ่ง คือด้านบวกหรือด้านลบเพียงด้านเดียว เพราะถ้าพิจารณาทั้งวัฏจักรจะได้ค่าเฉลี่ยเท่ากับศูนย์ ดังนั้นค่าเฉลี่ยจึงเป็นปริมาณทางไฟตรง พิจารณาตั้งแต่ 0 องศา ถึง 180 องศา



ค่าแรงดันใช้งาน (Effective Voltage) ปกติเมื่อนำมิเตอร์ไฟฟ้ากระแสสลับ เช่น AC.Voltmeter หรือ RMS. Voltmeter ไปวัดแรงดันไฟฟ้ากระแสสลับที่เต้ารับในบ้านจะอ่านค่าได้ 220 V เมื่อนำเครื่องมือวัดรูปร่างของรูปคลื่นไฟสลับ (ไซน์) ดังกล่าว เช่น นำออสซิลโลสโคปไปวัดจะได้รูปคลื่นไซน์

รายชื่อผู้จัดทำ

รายชื่อกลุ่ม

1. นาย วินเซนต์ ฟานตินี ม.6/2 เลขที่ 12



2. นาย เดชา เนื่องจำนงค์ ม.6/2 เลขที่ 24



3. นาย วรากร แซ่วู ม.6/2 เลขที่ 26




4. นาย ณัชณนนท์ กรเกี่ยว ม.6/2 เลขที่ 27



5. นาย ยงยศ ชูชื่นชัยมงคล ม.6/2 เลขที่ 33



*หมายเหตุ
รักมาสเตอร์ที่สุด จุ๊บบบๆ!! <3<3

ตัวอย่าง

ตัวอย่างและการอธิบาย

1. ถ้าปล่อยให้ก้อนหินตกจากยอดตึกสู่พื้น การเคลื่อนที่ของก้อนหินก่อนจะกระทบพื้นจะเป็นตามข้อใด ถ้าไม่คิดแรงต้านของอากาศ


ก. ความเร็วคงที่

ข. ความเร็วเพิ่มขึ้นอย่างสม่ำเสมอ

ค. ความเร็วลดลงอย่างสม่ำเสมอ

ง. ความเร็วเพิ่มขึ้นแล้วลดลง

แนวคำตอบ ข . วัตถุหล่นจากที่สูงด้วยความเร่งคงที่ คือ ค่าของ g เพราะฉะนั้น ความเร็วที่เกิดขึ้นก็ควรที่จะเพิ่มขึ้นอย่างต่อเนื่องตามความหมายของความเร่งนั่นเอง ดังนั้นคำตอบคือข้อ

2. โยนลูกบอลขึ้นไปในแนวดิ่งด้วยความเร็วต้น 4.9 เมตรต่อวินาที นานเท่าใดลูกบอลจึงจะเคลื่อนที่ไปถึงจุดสูงสุด


ก. 0.5 วินาที

ข. 1.0 วินาที

ค. 1.5 วินาที

ง. 2.0 วินาที

แนวคำตอบ ก. ตามโจทย์ที่ให้มานะครับไม่ต้องตกใจลองพิจารณาดี ๆ ก็จะรู้ว่าโจทย์ให้ค่าต่าง ๆ มาเพียงพอต่อการนำไปคำนวณนะครับ

โจทย์ให้ ความเร็วต้น คือ u = 4.9 m/s

ณ จุดสูงสุดเรารู้ค่าของความเร็วปลาย คือ v = 0 m/s

ค่าของความเร่งคือค่าของ g มีค่าเป็นลบเนื่องจากเคลื่อนที่ตรงข้ามกับ u มีค่า g = - 10 m/s2

โจทย์ต้องการหาค่าของ เวลาคือค่าของ t

เพราะฉะนั้นสิ่งที่เรารู้ u = 4.9 m/s , v = 0 m/s , g = -10 m/s2 , t = ? s

เราสารมารถใช้ สูตร v = u + gt

จะได้ 0 = 4.9 + (-10)t

t = 0.49 s

ดังนั้นคำตอบคือ 0.5 วินาที


3. รถยนต์คันหนึ่งเคลื่อนที่จากหยุดนิ่งไปบนเส้นทางตรง เวลาผ่านไป 4 วินาที มีความเร็วเป็น 8 เมตรต่อวินาที ถ้าอัตราเร็วเพิ่มขึ้นอย่างสม่ำเสมอ รถยนต์คันนี้มีความเร่งเท่าใด


ก. 2 เมตรต่อวินาทีกำลังสอง

ข. 4 เมตรต่อวินาทีกำลังสอง

ค. 12 เมตรต่อวินาทีกำลังสอง

ง. 14 เมตรต่อวินาทีกำลังสอง

แนวคำตอบ ก. ถ้าเราใช้ความรู้สึกหรืออ้างถึงความจริงแล้วเราก็สามารถหาคำตอบได้เลย คือ วัตถุอยู่นิ่งหมายความว่าความเร็วเริ่มต้นเป็น 0 เมตรต่อวินาที ถ้าเวลา 4 วินาที จะต้องเพิ่มความเร็วเท่าใดต่อ 1 วินาที จึงจะได้ 8 เมตรต่อวินาที ก็คือ เอาความเร็วปลายหารด้วยเวลาก็จะได้คำตอบเท่ากับ 2 เมตรต่อวินาทีต่อ 1 วินาที ก็คือ ความเร่งเท่ากับ 2 เมตรต่อวินาทีกำลังสองนั่นเองครับ ลองพิจารณาดี ๆ นะครับ ว่าจริงหรือเปล่า

ถ้าไม่แน่ใจก็ลองทำตามสูตรนะครับดังนี้

จากโจทย์ รถเคลื่อนที่จากหยุดนิ่งก็คือ ความเร็วต้น u = 0 m/s

เวลาในการเคลื่อนที่ t = 4 s

ความเร็วปลายของรถยนต์ในการเคลื่อนที่ v = 8 m/s

โจทย์ต้องการหาความเร่งของการเคลื่อนที่ คือ a

เพราะฉะนั้นสิ่งที่เรารู้คือ u = 0 m/s , t = 4 s , v = 8 m/s , a = ? m/s2

เราสามารถใช้สูตร v = u + at

8 = 0 + a(4)

a = 2 m/s2

ดังนั้นคำตอบคือ 2 เมตรต่อวินาทีกำลังสอง

ข้อสังเกตุง่ายๆในการคิด

ข้อสัีงเกตุแบบง่ายๆ


1.การตกเสรี ความเร่งคือ g เสมอ (จะเป็น 9.8 m/s2 หรือ 10 m/s2 แล้วแต่โจทย์กำหนด)
2.ที่จุดสูงสุด ความเร็วจะต้องเป็ง 0 (สังเกตุจากเมื่อเราโยนวัตถุขึ้นไป พอใกล้ๆ จะสูงสุด มันจะช้าลง พอสูงสุด มันจะนิ่ง แป๊ปนึง)
3.อย่าลืมกำหนดทิศทางเวลาคำนวน ที่จะสะดวกที่สุดก็คือ ขึ้นเป็น + ลงเป็นลบ ให้คงค่านี้ไว้แล้วจะไม่งง(แต่ถ้าเราโปรพอแล้ว ก็อาจจะกำหนดว่า ให้ทิศเดียวกะ U เป็น + ก็ได้ ตรงข้ามกับ U เป็น - หมด

*อย่าลืมว่าการคิดในนี้ต้องใช้การกระจัด เป็นหลัก ถ้า วัตถุลอยขึ้นแล้วตกถึงพื้น แสดงว่าการกระจัดเป็น 0

สมการการเคลื่อนที่แนวดิ่ง

สมการการเคลื่อนที่แนวดิ่ง

เนื่องจากการเ้คลื่อนที่แนวดิ่งนั้นคือการเคลื่อนที่ในแนวเส้นตรงแบบหนึ่ง สมการในการคำนวณจึงเหมือนกับสมการในการเคลื่อนที่แนวราบ เพียงแต่เปลี่ยนค่า a เป็น g เท่านั้น

u คือ ความเร็วต้น (m/s)

v คือ ความเร็วปลาย (m/s)

g คือ ความเร่ง (m/s2)

t คือ เวลา (s)

s คือ การกระจัด (m)




การกำหนดทิศทางของ g ซึ่งเป็นความเร่งเนื่องจากแรงโน้มถ่วงของโลก โดยปกติ g จะมีทิศลงเสมอ จึงถือว่าวัตถุเคลื่อนที่ลงให้ g เป็นบวก วัตถุเคลื่อนที่ขึ้นให้ g เป็นลบ


เมื่อวัตถุที่ตกแบบเสรี วัตถุจะเคลื่อนที่ลงด้วยความเร่ง g ถ้ากำหนดให้g = 10 m/s2 แสดงว่าวัตถุจะเคลื่อนที่ลงมาด้วยความเร็วเพิ่มขึ้นวินาทีละ 10 เมตรต่อวินาที แต่ถ้าโยนวัตถุนี้ขึ้นในแนวดิ่งวัตถุจะเคลื่อนที่ขึ้นช้าลงความเร่ง –g ถ้าg = 10 m/s2 จะได้ว่าวัตถุจะเคลื่อนที่ขึ้นด้วยความเร็วลดลงวินาทีละ 10 เมตรต่อวินาที จนกระทั่งความเร็วสุดท้ายเป็น 0 เรียกตำแหน่งนี้ว่า ตำแหน่งสูงสุดของการเคลื่อนที่ของวัตถุ หลังจากนี้วัตถุจะเคลื่อนที่ตกแบบเสรี

การเคลื่อนที่แนวดิ่ง

การเคลื่อนที่แนวดิ่ง

กาลิเลโอ ได้ทำการทดลองให้เห็นว่า วัตถุที่ตกลงสู่พื้นโลกอย่างอิสระ จะเคลื่อนที่ภายใต้แรงดึงดูดของโลก ต่อมานิวตันสังเกตุเห็นว่า ทำไมดวงจันทร์ไม่ลอยหลุดออกไปจากโลก ทำไมผลแอปเปิ้ลจึงตกลงสู่พื้นดิน นิวตันได้ทำการศึกษาค้นคว้าต่อ จนในที่สุดก็สามารถพิสูจน์ในเรื่องกฎแห่งการดึงดูดของ สสาร โดยโลกและดวงจันทร์ต่างมีแรงดึงดูดซึ่งกันและ กัน แต่เนื่องจากดวงจันทร์โคจรรอบโลก จึงมีแรงหนีสู่ศูนย์กลางซึ่งต่อต้านแรงดึงดูดไว้ ทำให้ดวงจันทร์ลอยโคจรรอบโลกได้ แต่ผลแอปเปิ้ลกับโลกก็มีแรงดึงดูดระหว่างกัน ผลแอปเปิ้ลเมื่อหลุดจากขั้วจึงเคลื่อนที่อิสระตามแรงดึงดูดนั้น




การตกอย่างอิสระนี้ วัตถุจะเคลื่อนตัวด้วยความเร่ง ซึ่งเรียกว่า Gravitational acceleration หรือ g ซึ่งมีค่าประมาณ 9.8 m/s